Reading Lists
The General Crisis of the 17th Century
Turchin’s Secular Cycles as background. Fischer’s The Great Wave as monetary history. Stone’s The Crisis of the Aristocracy for the effects on elites in England, and some interesting time-series; here’s one on the inflation of Peerage titles, re elite competition:
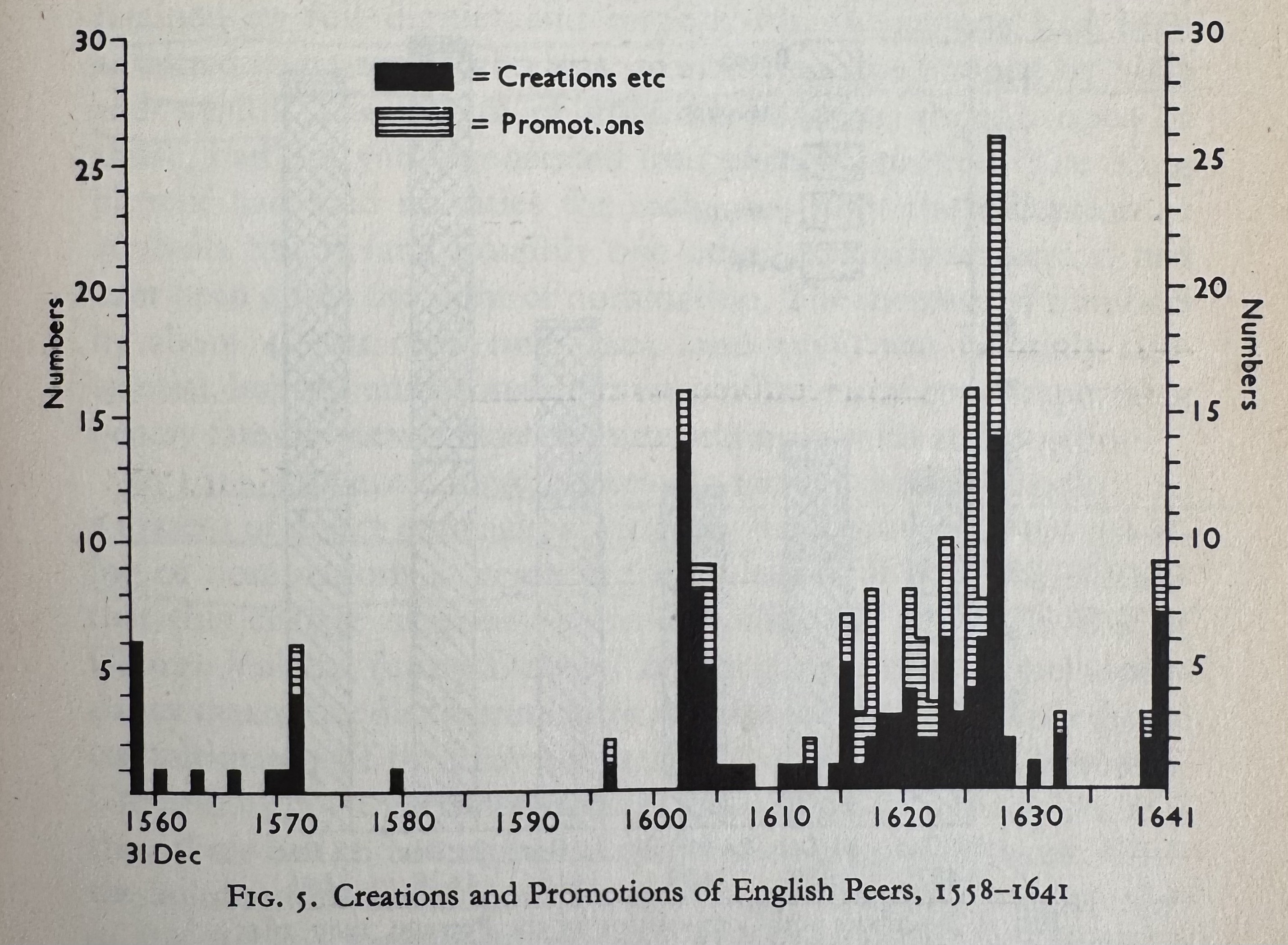
Bitton’s The French Nobility in Crisis for the same stuff in France. Jonathan Scott’s England’s Troubles for background on the English Civil War.
Staloff’s The Making of an American Thinking Class and the East Anglia section of Albion’s Seed for Puritanism in Massachusetts.
The best biographies are the autobiographies of his friends. Stanislaw Ulam’s Adventures of a Mathematician. Eugene Wigner’s Recollections. Goldstine’s The Computer from Pascal to von Neumann is also good. For a childhood account, John von Neumann as Seen by his Brother.
Anti-recommendation: The MANIAC.
1960s Counterculture — What Went Wrong?
Perlstein’s Nixonland as background. (Perlstein obviously hates Nixon, but the book is good anyway.) Joan Didion’s Slouching Towards Bethlehem for flavor. Roszak’s The Making of a Counter Culture for contemporary theorizing. Markoff’s What the Dormouse Said for effects on the nascent PC industry. Burrough’s Days of Rage for aftermath in the 1970s. Anderson’s The Upstart Spring for foreshadowing in the 1950s with emphpasis on the Esalen and the Human Potential Movement.
The first Chapter of David Brooks’ Bobos in Paradise or this SSC review on the “circulation of elites” in the 1960s. Cf the last chapter (“The X Way Out”) of Fusell’s Class and Cyra McFadden’s Serial. Also recommended: excerpts about the “Eloi” in J Storrs Hall’s Where Is My Flying Car?. See also Nicholas Lemann’s The Big Test for the SSC SAT hypothesis.
Frazer’s The Golden Bough is the essential book; read the Diana Nemorensis intro and decide how much more you want. See also Luc de Heusch.
On the story of Isaac, Shalom Spiegel’s The Last Trial. As historical background/commentary, Bergmann’s In the Shadow of Moloch.
The 1990s Internet
Brian McCullough’s How the Internet Happened as a sort of expanded index of events. On Netscape, Jim Clark’s Netscape Time and Michael Lewis’s The New New Thing. On PayPal, by far the best book is Soni’s The Founders. On Ebay, The Perfect Store.
Maggie Mahar’s Bull. Zac Bissonnette’s The Great Beanie Baby Bubble for a truly insane story.
Math
There are a lot of bad textbooks. Here are some good ones.
For single variable analysis: start with Abbott’s Understanding Analysis and then read baby Rudin.
Linear algebra: Strang’s Linear Algebra Done Right.
For multi-variable analysis, start with an “applied” book such as Marsden and Tromba. You wont understand any of the theory unless you can actually calculate. Then read the Hubbards’ Unified Approach. Spivak’s Calculus on Manifolds is an info-hazard, but if you read these two books first, you’re innoculated.
Once you’ve done the above on single, multi, and linear algebra, I highly recommend reading Edwards’ The Historical Development of the Calculus. You’lll get a lot of intuition.
Fourier analysis: Stein & Shakarchi.
Single-variable complex analysis: Conway, and then Stein & Shakarchi. Needham’s Visual Complex Analysis is a good secondary read. The reality is that the analytical perspective—identifying a function with its power series and worrying about convergence later—is pedagogically correct. Conway is the closest thing to that amongst modern textbooks.
Real analysis: Stein & Shakarchi. It’s the best book in the series.
Manifolds: Don’t read about manifolds. Unless you’re a specialist, the formal theory is a lot of work for very little payoff. The informal theory is just the multivariable analysis stuff that you already know.
Once you know some fourier, real, and complex analysis, read Jeremy Gray’s The Real and the Complex. Again, you’ll get a lot of intuition.
Differential equations: Don’t read about differential equations.
Stochastic differential equations: The only good theory book is Steele’s Stochastic Calculus and Financial Applications. If you want to actually calculate anything, Särkkä and Solin. See also, by yours truly.
General topology: Don’t read about general topology, just skip to algebraic topology instead.
Mesure theory: Don’t read about measure theory, read Stein’s Real Analysis instead.
Algebraic topology: Go to the library and skim Hatcher, just to see what the key theorems are. You won’t learn how to prove anything, but you’ll know the waypoints. Then read Rotman. The right start in algebraic topology is to [1] do homology the easy way with CW-complexes and cellular homology, and then [2] do things the category-theory way with singular homology.
Commutative algebra: Atiyah & Macdonald is a classic for a reason. Skip Eisenbud.
Introductory number theory: Ireland & Rosen’s A Classical Introduction to Modern Number Theory is great; you won’t read all of it on a first pass, and you don’t need to. For a first book inalgebraic number theory, Marcus’s Number Fields. Elliptic curves? Start with Silverman & Tate. Analytic NT? Start with Apostol.
For number theory history, read Edwards’ Fermat’s Last Theorem
Galois theory is one of those subjects (like manifolds, like measure theory, like topology) that suffers from over-formalization. To fight this, start with Edwards’ Galois Theory first. Then either Dummit & Foote or Roman’s Field Theory will be much more interesting.
Probability theory: Don’t read about formal probability theory. If your book has more than 10 page on sigma algebras, you’ve made a horrible mistake. Instead: read Casella & Berger’s Statistical Inference and Efron & Hastie’s Computer Age Statistical Inference.
Specific Histories that are Great
Forest and Sea Power: The Timber Problem of the Royal Navy, 1652-1862
Michael Knox Beran’s WASPS